伊豆大島から見える富士山を始め、美しい曲線が身の回りにみられます。その形に秘められた意味はなんでしょうか?

カテナリーcatenary曲線は日本語で懸垂線と呼ばれ、糸などを水平に張った時に自重でたわんだ曲線のことです。数学的には下記の関数で定義されます。

原点付近でマクローリン展開~{1})を行って、以下の2次関数で近似することもできます。
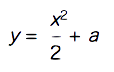
糸のように曲がりやすい構造物が自重で変形する際、各部には引張りのみが作用して、カテナリー曲線が描かれます。一方、石積みのアーチように各部に圧縮のみを作用させる構造にもこの曲線は適用されます。
送電線では、200-500m間隔の鉄塔で支えられており、電線の自重で均一な荷重(等分布荷重)が作用し、大きくたわんだ状態となります(図1)。

- 拡大
- 図1. たわむ送電線
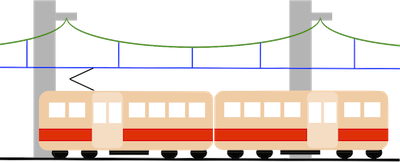
電車の架線では、250m程度の間隔で支持されていますが(図2)、そのたわみが大きくなると走行する電車のパンタグラフとの接触が維持できずに離れてしまい、給電が途切れてしまいます。その間にアーク放電~{2})が起こりやすくなり、好ましい状態ではなくなります。
- 拡大
- 図2. 直線架線を維持するメカニズム
そこで、カテナリー吊架(ちょうか)と呼ばれる方法で送電線を吊ることで架線を一定の高さに維持されるようにしています。最近では車両の移動速度の高速化に伴って、より複雑な吊架方法がとられています(図3)。
![図3. 電車の架線の支持方法(上はシンプルカテナリー式[時速100km程度まで],下はコンパウンドカテナリー式[時速160km程度まで])](/mirai/ja/achiv/dat_catenary/main/01/teaserItems1/02/binaryNodeName/catenary_fig3-1.png)
- 拡大
- 図3. 電車の架線の支持方法(上はシンプルカテナリー式[時速100km程度まで],下はコンパウンドカテナリー式[時速160km程度まで])
カテナリー曲線のもつ美しさから,建築構造物に適用した多くの例があります。
- 拡大
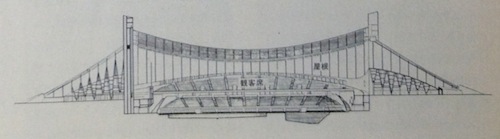
- 図4-1. 代々木第一体育館の構造図(『丹下健三 時代を映した“多面体の巨人 日経アーティテクチュア 1975-2005』日経アーティテクチュア. p65)
- 拡大
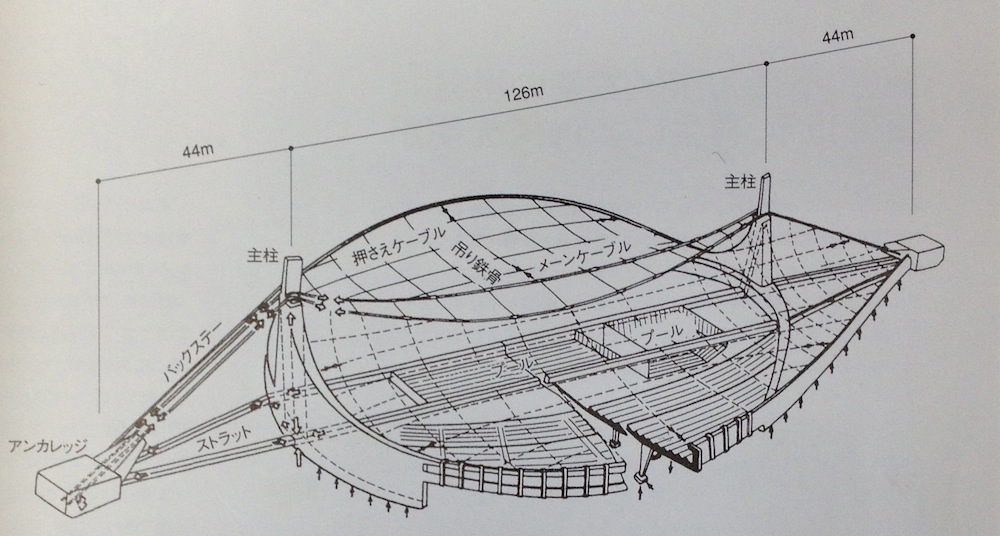
- 図4-2. 代々木第一体育館の構造図(『丹下健三 時代を映した“多面体の巨人” 日経アーティテクチュア 1975-2005』日経アーティテクチュア. p61)
図4-1は1964年に竣工した代々木第一体育館です。丹下健三氏の設計による吊り屋根構造が特徴的な建築物です。図4-2から分かるように、2本の主柱から張られた2本のメイン・ケーブルで吊橋状の中央構造を作り、さらにそこから吊り屋根面を形成しています。できあがった屋根はカテナリーを組合せた形をなし、内部の床面に柱のない空間を可能にしました。この代々木体育館は、1964年に東京オリンピックの会場として使われています。

- 拡大
- 図4-3. 代々木第一体育館内の様子(『丹下健三 時代を映した“多面体の巨人” 日経アーティテクチュア 1975-2005』日経アーティテクチュア. p174)
なお、この建築物には台風などによる屋根の揺れを低減するための油圧ダンパー(制振ダンパー)が日本で初めて用いられたそうです。ちなみに、最近の高層建造物では、地震による長周期振動を低減するために、油圧ダンパーに加えて種々の制振装置が付いています。
新しい建築構造物だけでなく、歴史的な建物にもカテナリー曲線はみられます。図5は寺社の屋根の輪郭にみられるカテナリー曲線です。富士山の輪郭もこれに近いのかもしれません。

- 拡大
- 図5. 寺社の屋根に見るカテナリー曲線(伊勢神宮内宮 神楽殿)
岩国にある錦帯橋(1673年)は曲線がきれいな橋で、その中央の3連は迫持式(せりもちしき)といわれるアーチ構造を形作っています(図6)。

- 拡大
- 図6. 錦帯橋の全体構造
このアーチ構造にもカテナリー曲線が適用されています。木材をこのような構造に加工するのは必ずしも容易ではなく、複数の板材を楔(くさび)で角度を変えながら重ねた後に帯鉄(おびがね)で束ねて、アーチを形成しているとのことです(図6)。なお,橋は木材のみで作られているわけではなく、鉄製の和釘や「かすがい」が多く使われています。
国内で石造りアーチ構造がもっとも多いのは九州です。中でも有名なものは熊本にある「通潤橋」と呼ばれる水道橋です。必ずしもカテナリー曲線には見えないかもしれませんが、力学的に安定な構造になっています。

- 拡大
- 図7. サグラダ・ファミリア教会のアーチに見られるカテナリー曲線(右図) (『ビジュアル版 西洋建築史 デザインとスタイル』長尾重武/星 和彦編 丸善株式会社. p135)
石のアーチ構造は古くからあります。スペイン・バルセロナにあるサグラダ・ファミリア教会は複雑な形状で知られており、ここでも一部のアーチ構造がカテナリー曲線状になっています(図7右)。
大島にあるシェルターの断面もアーチ状になっています(図8)。国内にある石造りアーチ構造は、サグラダ・ファミリア教会のアーチに比べて円形に近い形です。

- 拡大
- 図8. 大島三原山のシェルター
教会にみられるアーチ構造は主に上からの力を支えるものであるのに対し,国内にみられるアーチ構造は、側方からの力に対しても高い強度を持つという点で合理性があります。
1) マクローリン展開:関数f(x)を多項式で近似する方法であり、その多項式は関数fのx = 0における微分係数を用いて表現される。
2) アーク放電:電弧放電とも呼ばれ、弧を描きながら連続的に空気中を電子が移動する現象であり、高い温度を発生するため金属を溶かすこともでき、溶接にも用いられる。
アーチ構造 / カテナリー曲線 / 建造物 / 建築 / 曲線